Põhiline võrguteoreemid võrguanalüüsis kasutatavad on saadaval erinevat tüüpi, nagu Thévenin, superpositsioon, Norton, asendus, maksimaalne jõuülekanne, vastastikkus ja Millmani teoreemid . Igal teoreemil on oma rakendusalad. Seega on iga võrguteoreemi mõistmine väga oluline, kuna neid teoreeme saab erinevates ahelates korduvalt kasutada. Need teoreemid aitavad meil lahendada keerulisi võrguahelaid antud tingimuse jaoks. Selles artiklis käsitletakse üht võrguteoreemi tüüpi asendusteoreem – näiteid.
Mis on asendusteoreem?
Asendusteoreemi väide on; et kui vool kogu harus või pinge võrgu mis tahes harus on teada, saab haru muuta erinevate elementide kombinatsiooniga, mis loovad sarnase pinge ja voolu kogu selles harus. Teisisõnu võib seda määratleda kui; nii soojuspinge kui ka vool peaksid haru samaväärsuse huvides olema identsed.
Asendusteoreemi kontseptsioon sõltub peamiselt ühe elemendi asendamisest teise elemendiga. Sellest teoreemist on palju abi ka mõne teise teoreemi tõestamisel. Kuigi see teoreem ei ole rakendatav teoreemi lahendamiseks, mis hõlmab kahte ülaltoodud allikat, mis ei ole ühendatud ei järjestikku ega paralleelselt.
Asendusteoreemi seletus
Asendusteoreemi lahendamise etapid hõlmavad peamiselt järgmist.
Samm 1: Esiteks peame leidma kõigi võrguelementide pinge ja voolu. Üldiselt saab pinget ja voolu arvutada oomiseaduse abil, Kirchoffi seadused nagu KVL või KCL.
2. samm: Valige vajalik haru, mille soovite eemaldada mõne muu elemendi kaudu, nagu pingeallikas/takistus ja vooluallikas.
3. samm: Leidke asendatud elemendi õige väärtus tingimusel, et pinge ja vool ei tohiks muutuda.
4. samm: kontrollige uut vooluahelat, arvutades lihtsalt kõigi elementide voolu ja pinge ning hinnake seda algse võrgu järgi.
Asendusteoreemi skeem
Mõistame hõlpsasti asendusteoreemi, kasutades järgmist skeemi. Teame, et asendusteoreem on ühe elemendi asendamine teise samaväärse elemendiga. Kui mõni võrgu element asendatakse/asendatakse vooluallika või pingeallikaga, mille vool ja pinge elemendis või üle selle jäävad muutumatuks nagu eelmine võrk.
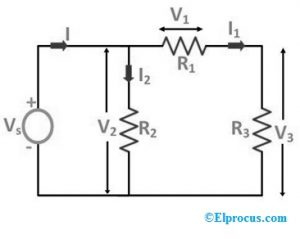
Erinevad takistused nagu R1, R2 ja R3 on ühendatud lihtsalt üle pingeallika. Kogu vooluringis voolav vool 'I' jaotatakse I1 ja I2, kus 'I1' toidetakse kogu 'R1' takistuse ulatuses ja 'I2' voolab läbi kogu takistuse R2, nagu on näidatud vooluringis. Siin on pingelangused takistustel R1, R2 ja R3 vastavalt V1, V2 ja V3.
Nüüd, kui takistus 'R3' asendatakse pingeallikaga 'V3', nagu on näidatud alloleval skeemil:
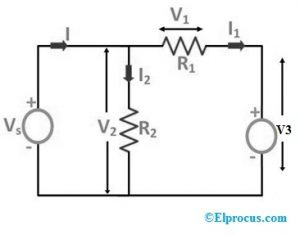
Järgmisel lülitusskeemil asendatakse takistus 'R3' voolu vooluga läbi selle elemendi 'I1'.
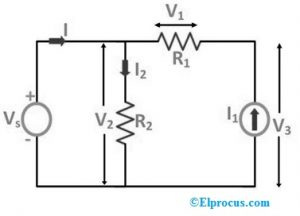
Ülaltoodud kahel juhul, kui element asendatakse voolu- või pingeallikaga, siis vooluahela algtingimused ei muutu, mis tähendab, et takistuse ja voolu toitepinge kogu takistuse ulatuses ei muutu isegi siis, kui need asendatakse muuga. allikatest.
Näidisprobleemid
Allpool käsitletakse asendusteoreemi näite probleeme.
Näide1:
Kõigi takistite pinge ja voolu arvutamiseks lahendage järgmine ahel asendusteoreemiga.
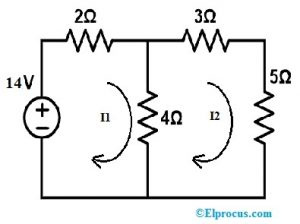
Samm 1:
Kõigepealt rakendage ülaltoodud ahelas loop1 KVL-i
14 = 6I1 – 4I2 ….(1)
Rakendage ülaltoodud ahelas loop2-le KVL-i
0 = 12I2 – 4I1
12 I2 = 4I1 => I1 = 3I2……….(2)
Asendage see võrrand 2 ülaltoodud võrrandis 1.
14 = 6(3I2) - 4I2
14 = 18I2 – 4I2 =>14I2 => 1A
I2 = 1A
Ülaltoodud võrrandist (2)
I1 = 3I2
Teame, et I2 = 1A
I1 = 3A
2. samm:
Selles etapis peame eemaldama loop1 oksad, et luua üks silmus.
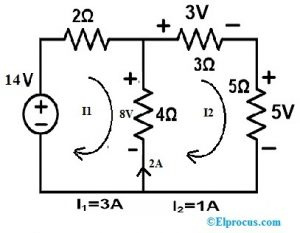
3. samm:
4Ω takisti asemel saame paigutada vooluallika/pingeallika. Nüüd kasutame praegust allikat.
Voolu vool kogu ahelas 2 on 1A. Seega asendame haru 1A vooluallikaga. Selle tulemusena on jääkvooluahel näidatud allpool.
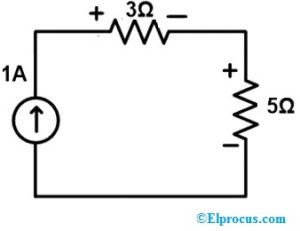
4. samm:
Selles etapis peate kontrollima kõigi elementide pinget ja voolu. Ülaltoodud ahel sisaldab ühte silmust, st vooluallikat. Seega on kogu ahelas voolava voolu väärtus sarnane vooluallika väärtusega.
Siin on vooluallika väärtus 1A. Seega on voolu vool 3Ω ja 5Ω takisti harudes 1A, mis on sarnane algse võrguga.
Kasutades oomi seadus , leidke 3Ω takisti pinge väärtus
V = IS
V = I x R
V = 1 x 3 => 3 V.
Samamoodi, kasutades oomi seadust, peame leidma 5Ω takisti pinge väärtuse.
V = IS
V = I x 5
V = 1 x 5 => 5 V.
Seega on vool ja pinge sarnased algse võrguga. Niisiis, see teoreem töötab nii.
Nüüd, kui valime 3. etapis vooluallika asemel pingeallika. Nii et selles olukorras on pingeallika väärtus sarnane 4Ω takisti haru väärtusega.
Voolu vool kogu 4Ω takisti harus algses võrgus on
I1 – I2 => 3 – 1 => 2A
Ohmi seaduse järgi;
4Ω takisti pinge on V = 2 x 4 = 8V
Seega peame ühendama võrgu pingeallika 8 V-ga ja jääkvooluahel on näidatud alloleval diagrammil.
V = 2 x 4 = 8 V
Seega peame ühendama 8 V pingeallika võrguga ja ülejäänud vooluring on selline, nagu on näidatud alloleval joonisel.
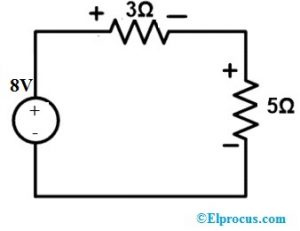
Pinge ja voolu kontrollimiseks rakendage ülaltoodud ahelale KVL-i.
8 = 3I + 5I => 8I
I = 1A.
Ohmi seadust kasutades saab takisti 3Ω pinge arvutada järgmiselt;
V = 1 × 3 => 3 V
Samamoodi on takisti 5Ω pinge;
V = 1 × 5 => 5 V
Seega on pinge ja vool pärast asendamist samad, mis algsel võrgul.
Näide2:
Võtame asendusteoreemi rakendamiseks järgmise ahela.
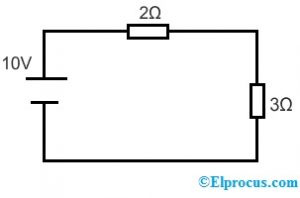
Pingejaotuse joonlaua järgi on 2Ω ja 3Ω takistite pinge;
3Ω takisti pinge on
V = 10 × 3/3 + 2 = 6 V
2Ω takisti pinge on
V = 10 × 2/3 + 2 = 4 V
Voolu voolu kogu ahelas arvutatakse I = 10/3+2 = 2A.
Kui asendame ülaltoodud ahelas 3Ω takisti asemel 6 V pingeallika, muutub vooluahel järgmiseks.
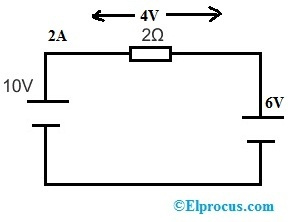
Ohmi seaduse alusel on pinge 2Ω takistil ja vooluhulk kogu ahelas
V = 10-6 => 4 V
I = 10-6/2 = 2A
Kui asendame 3Ω takisti asemel 2A vooluallika, muutub vooluahel järgmiseks.
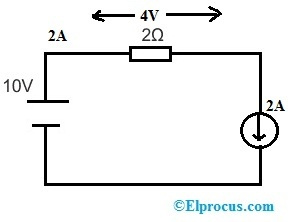
Pinge 2Ω takistil on V = 10 – 3* 2 => 4 V ja pinge 2A vooluallikas on V = 10 – 4 => 6 V. Seega ei muutu pinge 2Ω takistil ja vool kogu vooluringis.
Eelised
The asendusteoreemi eelised sisaldama järgmist.
- See teoreemi kontseptsioon sõltub peamiselt ühe elemendi asendamisest teise elemendiga.
- See teoreem annab intuitsiooni ahela käitumise kohta ja aitab kontrollida ka mitmesuguseid muid võrguteoreeme.
- Selle teoreemi kasutamise eeliseks on see, et see teoreem annab õiged väärtused muutujatele, nagu X ja Y, mis vastavad lõikepunktile.
Piirangud
The asendusteoreemi piirangud sisaldama järgmist.
- Seda teoreemi ei saa kasutada võrgu lahendamiseks, mis sisaldab vähemalt kahte või enamat allikat, mis ei asu järjestikku/paralleelselt.
- Selles teoreemis ei tohiks elemendi asendamisel ahela käitumine muutuda.
Rakendused
The asendusteoreemi rakendused sisaldama järgmist.
- Asendusteoreemi kasutatakse paljude teiste teoreemide tõestamiseks.
- See teoreem on abiks matemaatika võrrandisüsteemi lahendamisel.
- See teoreem asendab ahela ühe elemendi veel ühe elemendiga.
- Seda teoreemi kasutatakse sõltuvate allikatega ahelate analüüsimiseks.
Millise vooluahela asendusteoreem ei kehti?
Ahel, millel on kaks ülaltoodud allikat, mis on ühendatud kas paralleelselt või järjestikku, siis see asendusteoreem ei kehti.
Miks nimetatakse kompensatsiooni teoreemi asendamiseks?
Mõlemad teoreemid, nagu kompenseerimine ja asendamine, on protseduuri ja redutseerimise osas identsed. Seega on see teoreem rakendatav antennide puhul ja seda nimetatakse ka asendusteoreemiks.
Kuidas kasutate asendusteoreemi?
Seda teoreemi saab kasutada, asendades võrgu mis tahes haru mõne teise haruga, ilma et see häiriks pingeid ja voolusid kogu võrgus. Seega kasutatakse seda teoreemi nii lineaarsetes kui ka mittelineaarsetes ahelates.
Mis on asendusomand?
Asendusomadus sätestab, et kui muutuja 'a' on samaväärne teise muutujaga 'b', saab 'a' asendada 'b' asemel mis tahes avaldises või võrrandis ja 'b' saab asendada 'b' asemel. a' mis tahes avaldises või võrrandis.
Seega on see kõik umbes asenduse ülevaade teoreem – skeem koos näidetega. Siin on teile küsimus, mis on kompensatsiooni teoreem?