Enne Heisi silla arutamist peame teadma Maxwelli kohta sild piirangud, et mõista, kuidas seda silda paljudes rakendustes kasutatakse. Maxwelli silla põhiülesanne on mõõta mähiste keskmist QF (kvaliteeditegurit) (1 Definitsioon: Silla vooluringi, mida kasutatakse suure Q-faktoriga mähiste takistuse ja induktiivsuse mõõtmiseks, nimetatakse Hays Bridge'iks. See on modifikatsioon Maxwelli oma sild. Niisiis kasutatakse seda silda vooluahela kvaliteetse teguri määramiseks. heinad-sild Heina sillaahelate ühendamine toimub kondensaatori ja takisti järjestikku ühendamise teel. Nii, et takistuse ja mahtuvuse pingelangust muudetakse. Maxwelli sillas on ühendus vastupanu & mahtuvust saab teha paralleelselt. Seetõttu on pingeallika suurus kogu ulatuses takisti & kondensaator on sama. Hayesi silla ehitus on näidatud allpool. Järgmises vooluringis ei ole 'L1' induktor tundmatu ja see on paigutatud takistusega 'R1' ab-käe vahele. Selle induktori võrdlust saab teha kondensaatoriga „C4”, mis on ühendatud „R4” takistusega cd-harus. Samamoodi on ülejäänud takistused, nagu R2 ja R3, ühendatud harudes ad & bc. heina-silla ehitus Silla tasakaalustatud seisundis saamiseks reguleeritakse nii ‘R4’ takistust kui ka ‘C4’ kondensaatorit. Kui vooluahel on tasakaalus, ei toimu detektoris voolu. Siin asetatakse detektor b & d vahele. Potentsiaalne langus reklaami- ja CD-rühmas on võrdne. Samamoodi on potentsiaalne langus ab & bc harus samaväärne. Ülaltoodud vooluahelas on induktor L1 tundmatu induktor, sealhulgas R1 takistus R2, R3, R4 on tuntud kui induktiivne resistentsus. ‘C4’ on tavaline kondensaator Ülaltoodud silla koormustakistused on Z1 = R1-j / ωc1 Z2 = R2 Z3 = R3 Z4 = R4 + jωL4 Kui vooluring on tasakaalus Z1Z4 = Z2Z3 Asendage ülaltoodud võrrandites koormuse impedantsid (R1-j / ωc1) * (R4 + jωL4) = R2 * R3 Siin 1 / C1 = L1 ja L4 = 1 / C4 R1R4 + R1jωL4 - jR4 / ωc1 + jωL4 / ωc1 = R2 * R3 R1R4 + L1 / C4 + jωL1R4-jR1 / ωc4 = R2 * R3 Kui tegelikud ja kujuteldavad mõisted on lahutatud, saame järgmise R1R4 + (L1 / C4) = R2 * R3 jωL1R4- (jR1 / ωc4) = R2 * R3 Eespool toodud võrrandite lahendamisel saame L1 = R2R3C4 / (1+ ω2R42C42) R1 = ω2C42R2R3R4 / ω2R42C42 Mähise QF on Q = ωL1 / R1 = 1 / ω2R4C4 Tundmatu mahtuvuse ja induktiivsuse võrrand sisaldab peamiselt sagedusperioodi. Seetõttu peab tundmatu induktiivsuse väärtuse leidmiseks olema teada toitesagedus. Siin ei mängi sagedus kõrge QF-i puhul olulist rolli Q = 1 / ω2R4C4 Selle väärtuse asendamine L1-ga L1 = R2R3C4 / 1 + (1 / Q) 2 Suure Q väärtuse korral võib 1 / Q eirata ja seega võrrand on L1 = R2R3C4 Järgmises Hayesi silla faasiskeemil on e1, e2, e3 ja e4 nullpunktid. Kui vool voolab läbi haru ‘bd’, siis e1 = e2 ja e3 = e4. Siin on ‘i1’ faasordiagrammi tugitelg ja see telg viib haru ‘cd’ vahele ühendatud kondensaatori tõttu teatud nurga all ‘i2’. Märkige nullpunkti e1 ja e2 tulemus e-ni. Faasinurk elektritakistuse (r4) ja kondensaatori (c4) vahel on joonisel näidatud 90 °. faas-diagramm Heina silla eelised on Heina silla puudused on Rakendused on Seega on see kõik ülevaade Hay sillast . Kvaliteeditegurit saab mõõta nii Maxwelli kui ka Hay silla abil, kuid Maxwelli kasutatakse keskmise QF (Q 10) arvutamiseks. Nii et Maxwelli piirangute ületamiseks kasutatakse seda sildahelat. Siin on teile küsimus, mis vahe on Maxwelli ja Hay silla vahel?Mis on Hays Bridge?

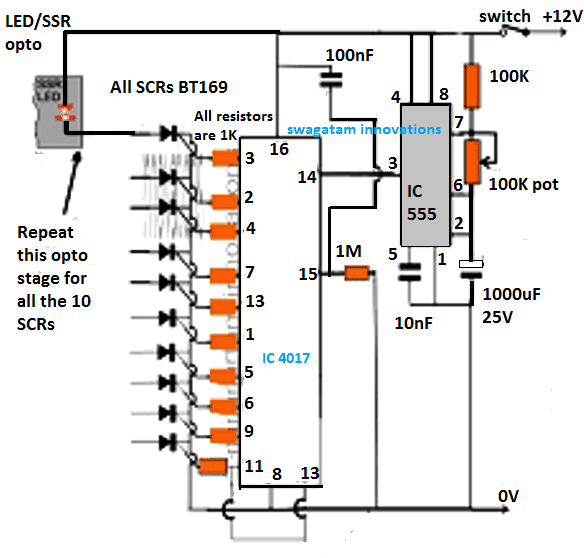
Heina silla ehitamine

Heina silla teooria
Hays Bridge'i faasiskeem

Eelised
Puudused
Hayesi silla rakendused