Lihtsa harmoonilise liikumise leiutas prantsuse matemaatik parun Jean Baptiste Joseph Fourier 1822. aastal. Edwin Armstrong (18. detsember 1890 - 1. veebruar 1954) jälgis oma katsetes võnkeid 1992. aastal ja Alexander Meissner (14. september 1883 kuni 3. jaanuar 1958) leiutas ostsillaatorid märtsis 1993. Mõiste harmooniline on ladinakeelne sõna. Selles artiklis käsitletakse harmoonilise ostsillaatori ülevaadet, mis sisaldab selle määratlust, tüüpi ja rakendusi.

Mis on harmooniline ostsillaator?

Harmooniline ostsillaator on määratletud kui liikumine, mille jõud on tasakaalupunktist otseselt proportsionaalne osakesega ja see toodab sinusoidaalse lainekuju kujul väljundit. Jõudu, mis põhjustab harmoonilist liikumine saab matemaatiliselt väljendada kui

F = -Kx

Kus

F = taastav jõud

K = kevadkonstant

X = kaugus tasakaalust

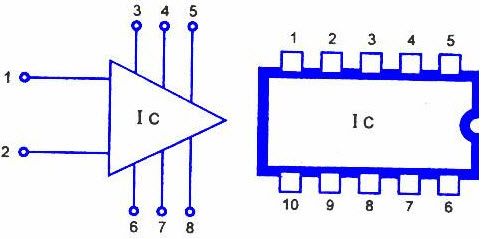
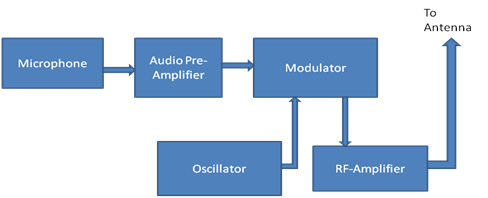
harmoonilise ostsillaatori plokkskeem

Harmoonilises liikumises on punkt, milles süsteem võnkub, ja jõud, mis toob massi ikka ja jälle samasse kohta, kust see algab, jõudu nimetatakse taastavaks jõuks ja punkti nimetatakse tasakaalupunktiks ehk keskmiseks positsiooniks. Seda ostsillaatorit tuntakse ka kui lineaarne harmooniline ostsillaator . Energia voolab aktiivsest komponendid passiivkomponentidele ostsillaatoris.

Blokeeri skeem

The harmoonilise ostsillaatori plokkskeem koosneb võimendi ja tagasisidevõrgustik. Võimendit kasutatakse signaalide võimendamiseks ning võimendatud signaalid suunatakse läbi tagasiside võrgu ja genereeritakse väljund. Kui Vi on sisendpinge, Vo on väljundpinge ja Vf tagasisidepinge.

Näide

Mass kevadel: Vedru annab massi kiirendava taastava jõu ja taastav jõud väljendub järgmiselt

F = ma

Kus ‘m’ on mass ja a on kiirendus.

“mitu tüüpi operatsioonisüsteeme ”

mass-kevadel

Vedru koosneb massist (m) ja jõust (F). Kui jõud tõmbab massi punktis x = 0 ja sõltub ainult x-st - massi asend ja vedrukonstant on täht k.

Harmoonilise ostsillaatori tüübid

Selle ostsillaatori tüübid hõlmavad peamiselt järgmist.

Sunnitud harmooniline ostsillaator

Kui rakendame süsteemi liikumisele välist jõudu, siis öeldakse, et liikumine on sunnitud harmooniline ostsillaator.

Summutatud harmooniline ostsillaator

See ostsillaator on määratletud nii, et kui rakendame süsteemile välist jõudu, siis ostsillaatori liikumine väheneb ja selle liikumine on väidetavalt summutatud harmooniline liikumine. Neid on kolme tüüpi summutatud harmoonilisi ostsillaatoreid

summutavad lainekujud

Üle sumbunud

Kui süsteem liigub aeglaselt tasakaalupunkti suunas, siis öeldakse, et see on üle summutatud harmooniline ostsillaator.

Damped all

Kui süsteem liigub kiiresti tasakaalupunkti suunas, siis öeldakse, et see on üle summutatud harmooniline ostsillaator.

Kriitiline summutatud

Kui süsteem liigub võimalikult kiiresti, ilma et tasakaalupunkt oleks võnkunud, öeldakse, et see on üle summutatud harmooniline ostsillaator.

Kvant

Selle leiutasid Max Born, Werner Heisenberg ja Wolfgang Pauli Göttingeni ülikoolist. Sõna kvant on ladinakeelne sõna ja kvant on väike energiahulk.

Nullpunkti energia

Nullpunkti energiat tuntakse ka kui põhiseisundi energiat. See on määratletud siis, kui põhiseisundi energia on alati suurem kui null ning selle kontseptsiooni avastas Max Planck Saksamaal ja 1990. aastal välja töötatud valem.

Summutatud lihtsa harmoonilise ostsillaatori võrrandi keskmine energia

On kahte tüüpi energiaid, need on kineetiline energia ja potentsiaalne energia. Kineetilise energia ja potentsiaalse energia summa on võrdne koguenergiaga.

E = K + U ………………. Eq (1)

Kus E = koguenergia

K = kineetiline energia

U = potentsiaalne energia

Kus k = k = 1/2 mv^kaks………… ekv (2)

U = 1/2 kx^kaks………… ekv (3)

võnketsükkel- keskmise väärtused

Kineetilise ja potentsiaalse energia keskmised väärtused võnketsükli kohta on võrdsed väärtusega

Kus v^kaks= v^kaks(TO^kaks-x^kaks) ……. ekv (4)

Eq (2) ja eq (3) asendavad ekv (4) saavad

k = 1/2 m [mass^kaks(TO^kaks-x^kaks)]

= 1/2 m [Aw cos (wt + ø₀)]^kaks……. ekv (5)

U = 1/2 kx^kaks

= 1/2 k [patt (wt + ø₀)]^kaks……. ekv (6)

Eq (1) asendajad eq (5) ja eq (6) saavad kogu energiaväärtuse

E = 1/2 m [mass^kaks(TO^kaks-x^kaks)] + 1/2 kx^kaks

= 1/2 m w^kaks-1/2 m w^kaksTO^kaks+ 1/2 kx^kaks

= 1/2 m w^kaksTO^kaks+1/2 x^kaks(K-mw^kaks) ……. ekv (7)

Kus mw^kaks= K , asenda see väärtus ekvivalendis (7)

E = 1/2 K A^kaks- 1/2 Kx^kaks+ 1/2 x^kaks= 1/2 K A^kaks

Koguenergia (E) = 1/2 KA^kaks

Ühe ajaperioodi keskmised energiad väljendatakse

TO_keskm= U_keskm= 1/2 (1/2 K A^kaks)

Harmoonilise ostsillaatori lainefunktsioon

Hamiltoni operaator on väljendatud kineetilise energia ja potentsiaalse energia summana ning see on väljendatud

ђ (Q) = T + V ………………. ekv (1)

Kus ђ = Hamitoni operaator

T = kineetiline energia

V = potentsiaalne energia

Lainefunktsiooni genereerimiseks peame tundma Schrodingeri võrrandit ja võrrandit väljendatakse

-đ^kaks/ 2μ * d^kaksѱ_υ(Q) / dQ^kaks+ 1 / 2KQ^kaksѱ_υ(Q) = E_υѱ_υ(Q) …………. ekv (2)

Kus Q = normaalkoordinaadi pikkus

Μ = efektiivmass

K = jõu konstant

Schrodingeri võrrandi piiritingimused on:

Ѱ (-∞) = ø

Ѱ (+ ∞) = 0

Võime ekv (2) kirjutada ka kujul

d^kaksѱ_υ(Q) / dQ^kaks+ 2μ / đ^kaks(E_υ-K / 2 * Q^kaks) ѱ_υ(Q) = 0 ………… ekv (3)

Võrrandi lahendamiseks kasutatud parameetrid on

β = ђ / √μk ……… .. ekv (4)

d^kaks/ dQ^kaks= 1 / β^kaksd^kaks/ dx^kaks………… .. ekv (5)

Asendage ekv (3) ekv (4) ja ekv (5), seejärel saab selle ostsillaatori diferentsiaalvõrrand

d^kaksѱ_υ(Q) / dx^kaks+ (2μb^kaksE_υ/ đ^kaks- x^kaks) ѱ_υ(x) = 0 ……… .. ekv (6)

Võimsuse seeria üldine väljend on

ΣC¬nx2 …………. ekv (7)

Eksponentsiaalset funktsiooni väljendatakse

exp (-x^kaks/ 2) ………… ekv (8)

eq (7) korrutatakse eq (8) -ga

ѱυ (x) = ΣC¬nx2exp (-x2 / 2) …………… ..ekv (9)

Hermiidi polünoomid saadakse allpool toodud võrrandi abil

ђ_υ(x) = (-1)^υ* exp (x^kaks) d / dx^υ* exp (-x^kaks) …………… .. ekv (10)

Normaliseeriv konstant väljendatakse

N_υ= (1/2^υυ! √Π)^1/2……………. Ekv (11)

The lihtne harmooniline ostsillaatori lahendus on väljendatud

Ѱ_υ(x) = N_υH_υ(ja) e^{-x2 / 2}……………… ekv (12)

Kus N_υon normaliseerimise konstant

H _υon Hermite

on ^{-x2 / kaks}on Gaussi

Võrrand (12) on harmoonilise ostsillaatori lainefunktsioon.

Selles tabelis on toodud kõige madalama energiaga olekute hermiidi polünoomid

^υ	0	1	kaks	3
H_υ(Y)	1	2a	4a^kaks- kaks	8a³-12a

Lainefunktsioonid lihtne harmooniline ostsillaatori graafik nelja madalaima energiaseisundi korral on näidatud allpool toodud joonistel.

lainefunktsioonid - harmooniline ostsillaator

harmoonilise ostsillaatori lainefunktsioonid

Selle ostsillaatori tõenäosustihedused nelja madalaima energiaseisundi korral on näidatud allpool toodud joonistel.

lainevormide tõenäosustihedused

Rakendused

Sharmooniline ostsillaatorrakendused hõlmavad peamiselt järgmist

Heli- ja videosüsteemid
Raadio ja muud sideseadmed
Inverterid , Äratused
Sumisevad
Dekoratiivsed tuled

Eelised

The harmoonilise ostsillaatori eelised on

Odav
Kõrgsageduslik genereerimine
Kõrge efektiivsusega
Odav
Kaasaskantav
Säästlik

Näited

Selle ostsillaatori näide sisaldab järgmist.

Muusikariistad
Lihtne pendel
Massvedru süsteem
Kiik
Kella käte liikumine
Auto, veoauto, busside jne rataste liikumine

See on üks liikumisliik, mida saame jälgida igapäevaselt. Harmooniline ostsillaator lainefunktsioon Schrodingeri abil ja tuletatakse harmoonilise ostsillaatori võrrandid. Siin on küsimus, millist liikumist benji-hüpped sooritavad?